II/ Se localiser grâce au temps

1) L’horloge atomique :

a.      Qu'est-ce qu'une horloge atomique ?

Une horloge atomique est une horloge très performante permettant de connaitre avec une précision phénoménale l’heure exacte sur Terre (une précision de l'ordre d'une nanoseconde, soit 10^-9s), avec une marge d’erreurs d'une seconde de décalage sur 15 milliards d’années.

Cette horloge, contrairement aux horloges habituelles, utilisent des atomes avec des oscillations à la fois rapides et régulières.

C’est au début des année 1950 que les horloges atomiques commenceront à connaitre des prototypes et à être assemblées. Ce n’est qu’en 1967 qu’elles vont prendre de l’ampleur avec la création TAI « Temps Atomique International » et l’UTC « Coordinated Universal Time », une nouvelle échelle de temps liée à l’horloge atomique.

Image d'une horloge atomique

LOUAPRE, David. [en ligne],https://sciencetonnante.wordpress.com/2013/03/04/sans-einstein-pas-de-gps/

b.      Fonctionnement d'une horloge atomique

Ici, on confine des atomes dans un endroit à très faible volume dans un environnement stable. On utilise une des fréquences de ces atomes que l’on excite via l'action d’une fréquence sur celle des atomes pour comparer la fréquence de l’oscillation de ces atomes avec celle de l’excitation qu’on lui apporte. A la suite de cela,  on ajuste la fréquence qui  fait action sur les atomes. On peut copier ces fréquences d’oscillations qui sont aussi régulières que celle des atomes et donc générer des secondes.

La seconde a une nouvelle définition :  9 192 631 770 d' oscillations de l’atome de césium 133 par l’horloge atomique.

Le fonctionnement de l’horloge atomique réside dans l’utilisation d’une fréquence d’un atome pour obtenir une précision parfaite.

Pour ce faire tout un dispositif est mis en place. On prend le modèle de l’horloge d’atome de césium ci-dessous comme exemple :

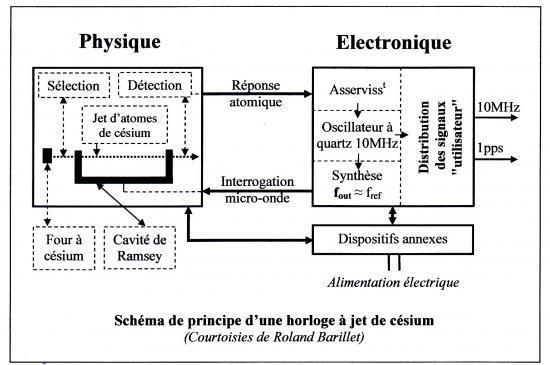
Système d'une horloge atomique

http://horlogeatomiquetpe.e-monsite.com/pages/le-fonctionnement-de-l-horloge-atomique.html [en ligne]

Plus précisemment, les atomes sont traités dans la cavité de Ramsey. Cette cavité contient un champs électromagnétique dont la fréquence est égal à la différence de 2 niveaux d'excitation : E₂ - E₁ , deux bras contenant des micro-ondes qui envoient 2 brèves impulsions et deux trous entre chaque bras permettant aux atomes de transiter les atome dans la cavité, et un four à césium qui envoit un jet d'atome dans la cavité. La première impulsion va  dévier les atomes dans un états A vers la cavité de Ramsey alors que les atomes dans un état B ne le seront pas. C'est un filtrage magnétique, qui séparent les atomes à différentes fréquences, c'est le niveau de sélection des atomes. Dans la cavité les atomes qui ont leur fréquence en accord avec les micro-ondes vont alors passer à un état éxcité noté B. Il est très important que l'exciation que subie l'atome par les micro-ondes soient de la même fréquence. A la sortie de la cavité il y un nouveau filtrage magnétique qui dévie cette fois les atomes dans un état B vers le niveau de détection et non ceux les atomes d'état A.

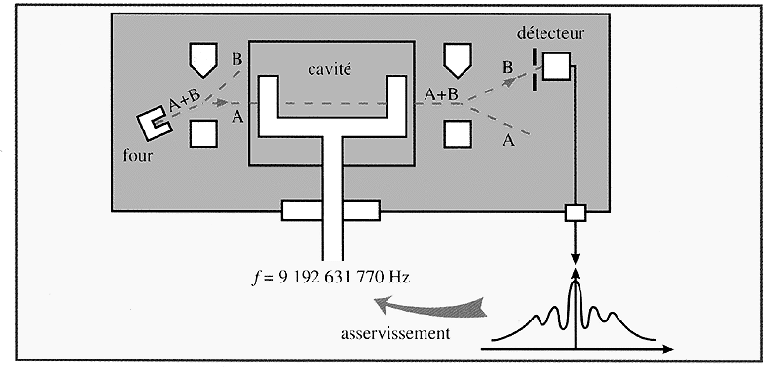
Fonctionnement du la cavité de Ramsey

http://perso.utinam.cnrs.fr/~vernotte/node6.html [en ligne]

Le niveau détection va compter le nombre d'atomes éxcités. Alors, la fréquence du quartz va s'adapter pour recevoir un maximum d'atomes excités. La fréquece obtenue est connue avec une grande précision et nous savons avec ecxactitude le nombre de cycles par seconde et par conséquent l'heure de l'holroge est déterminé par comptage de nombres de cycles. 

c.      Synchronisation des horloges atomiques

En effet, pour transmettre l'heure sur Terre les horloges atomiques transmettent les signaux via synchronisation entre horloges et récepteurs. Le problème étant que les horloges sont trop chères et trop volumineuses pour être installées dans les récepteurs. la communication se fait alors par signal. Les récepteurs et les horloges atomiques émettent tout les deux un signal de forme électrique

              <<- Signal électrique entre la Terre et le satellite ->>             

   https://fr.wikipedia.org/wiki/Fichier:UFO_satellite_2.jpg  [en ligne]                            https://fr.wikipedia.org/wiki/Fichier:La_Terre_vue_de_l%27Apollo_17.jpg [en ligne]                                                                                                                                                                                                       
Le récepteur effectue une comparaison entre son signal et celui de l'horloge dans le but de déterminer le décalage des signaux (décalage causé par la dilatation du temps, abordé dans le II 3.). Cela permet d'évaluer la distance entre le récepteur et les satellites qui ont émis le signal, du parcours du signal et mesurer le temps du parcours du signal. Pour la distance entre le récepteur et le satellite, on utlise la trilatération qui sera démontré dans le II 2.). Le parcours d'un signal électrique est en ligne droite, lorsqu'il rentre dans l'atmosphère terrestre, le signal est dévié car il change de milieu de propagation (plus de précision dans le III 2.b)

Aujourd’hui, des horloges toujours plus précises sont inventés. Récemment une horloge possédant une marge d’erreurs de 1 seconde sur 15 milliards d’année a été inventé. Cela est dû à une découverte d’atomes toujours plus stable ou une fréquence toujours plus efficace.

Par la suite nous verrons un des domaines où ces horloges sont utilisées et pourquoi leur rôle est si importants.

2) Se localiser avec la trilatération :

a.      La trilatération sur un plan (2D)

La trilatération est similaire à la triangulation, elle permet de déterminer la position d'un point, mais n’utilise que des calculs de distances, c’est-à-dire sans calcul d’angle.

Pour expliquer le principe de trilatération, imaginons qu’un phare « A » émet une lumière toutes les 10 secondes. Imaginons aussi que le voilier et le phare possèdent chacun une horloge atomique, synchronisées toutes les 2.

Quand le phare émet sa lumière par exemple à 17h10min, le voilier va voir la lumière à 17h10min et quelques µs. Le voilier pourra donc connaitre sa distance par rapport au phare A grâce à la formule :

D = V x dt 

(D en en m ; V en m/s ; dt en s)

avec

• D : la distance
• V pour la vitesse (ici celle de la lumière : c)
• dt le temps de propagation du signal

Si l’horloge indique un écart de 13,3 µs par rapport à la dernière fois qu’il y avait 10 secondes d’écoulées, on peut en déduire que le voilier est à 300 000 (km/s) * 13,3 10^-6 (s) = 4 km de distance du phare.

Le problème est que si le voilier n’arrive pas à reconnaitre quel phare lui a envoyé le flash lumineux (en temps de brouillard par exemple), le voilier saura qu’il est à 4 km d’un phare, mais il ne saura pas lequel !

Ce problème est réglé si le phare envoie un message radio « je suis le phare A » toutes les 10s. Ce message se propage lui aussi à la vitesse de la lumière c.

Enfin, si le phare indique dans son message l’heure à laquelle il envoie ce message, il n’est plus nécessaire que le phare et le voilier se mettent d’accord sur un envoi de messages toutes les 10 secondes par le phare. Le phare peut alors envoyer le message quand il veut (à t_A). En comparant avec son heure de réception (à t), le voilier sait alors calculer le temps de propagation : t- t_A

Avec cette information, le voilier sait juste qu’il est à 4 km du phare A, c’est-à-dire n’importe où sur le cercle de centre « Phare A » et de rayon 4km. A noter que le voilier à besoin de connaitre la position du phare A sur la carte.

En connaissant sa distance par rapport à un deuxième phare, sa position devient beaucoup plus précise, il ne reste plus que 2 possibilités (à l’intersection des 2 cercles):

Sa distance par rapport à un troisième phare permet au voilier de connaitre sa position exacte (à l’intersection des 3 cercles) :

En résumé, en connaissant sa distance à 3 phares, le voilier peut calculer sa position précise (à noter que le voilier doit connaitre préalablement la position de chacun de ces phares sur la carte)

b.      La trilatération dans l’espace (3D)

Suivant le même principe que les phares, les satellites GPS disposés autour de la terre embarquent des horloges atomiques et émettent des signaux radios (du type « je suis le satellite s₁ et il est t₁ ») qui permettent au récepteur GPS de se géolocaliser.

Contrairement aux phares, les satellites changent de position en permanence (environ 4m en 1ms). Le récepteur (R), grâce à l’almanach, calcule les positions approximatives (précision d’environ 1 km) des satellites. Les éphémérides sont des informations beaucoup plus précises (précision d’environ 1 m), et sont envoyés vers le récepteur par les satellites. Chaque satellite envoie donc un message du type « je suis le satellite s₁, il est t₁, et voici ma position précise ».

De plus, en pratique, il n’est pas possible d’embarquer une horloge atomique dans les récepteurs GPS. Pour résoudre ce problème, les satellites envoient des informations électroniques de synchronisation qui permet au GPS de se synchroniser précisément en comparant les informations qui lui arrivent de plusieurs satellites

Prenons le référentiel tridimensionnel orthonormé avec :

• l’origine le centre de la terre O,
• l’axe Oz est l’axe de rotation de la Terre, orienté vers le pôle Nord
• l’axe Oy passant par l’équateur et le méridien de Greenwich
• l’unité est 1 km

Les axes Ox et Oy forment un plan passant par l’équateur.

Le rayon r de la terre est environ 6371 km

Dans ce référentiel, on définit par (x,y,z) les coordonnées du récepteur R qui se trouve sur la surface de la terre. On ne peut toutefois pas en déduire que OR est environ 6371 km, car le récepteur peut se trouver par exemple en haut d’une montagne, ou dans un vallée, ou dans un avion! La terre n’est pas non plus une sphère parfaite. La distance OR ne doit donc pas être utilisé, car elle n’est pas connue exactement.

Chaque satellite envoie donc un message du type « je suis le satellite s1, il est t₁, et ma position précise est x₁,y₁,z₁ ». En recevant le signal d’un satellite à t, le récepteur est capable (comme pour les phares) de calculer à quelle distance il est du satellite :

(Équation 1)

Le récepteur en déduit qu’il se trouve quelque part sur la sphère de rayon D et ayant pour centre la position du satellite :

Avec deux satellites, on déduit que le récepteur est quelque part sur le cercle à l’intersection des 2 sphères :

Avec trois satellites, on déduit que le récepteur est quelque part sur un des 2 points à l’intersection du cercle (intersection des 2 premières sphères) et de la 3ieme sphère :

Un 4^ème satellite permet de déduire précisément la position du récepteur. Dans la pratique, avoir encore plus de satellites permet de connaitre encore plus précis la position (plus on a d’information, plus cela réduit les erreurs)

En résumé, pour déterminer sa position (x,y,z) dans le référentiel terrestre, un récepteur

• doit connaitre, au même instant t, sa distance par rapport à 4 satellites (grâce aux temps de propagation et à la synchronisation de ces 5 équipements),
• doit connaitre la position précise de ces 4 satellites

Le récepteur va pouvoir faire ce calcul grâce au théorème de Pythagore en exprimant la distance entre les satellites et le récepteur à l’aide de leurs coordonnées :

D’après le théorème de Pythagore, on sait que AB²+BC² = AC² et que AC²+CD² = AD²  

On a donc AD² = AB²+ BC² + CD²

Or :

donc :

(Équation 2)

Grâce aux Équation 1 et Équation 2, cela donne une première équation à résoudre :

(Équation 3)

Pour calculer sa position (x,y,z) avec l’aide de 4 satellites, le récepteur GPS doit donc résoudre les équations suivantes :

Avec t = le temps lorsque le signal arrive sur le récepteur (on considère que les 4 signaux arrivent en même temps, ce qui est possible car les satellites diffusent leur message en continue).

c.      Exemple de calcul de trilatération GPS

Partons des données suivantes, pour 4 satellites, et exprimées en km et ms.

Il faut donc aussi exprimer la vitesse de la lumière en km et ms : c = 299 792 km/s = 299,792 km/ms

Les distances en km entre le récepteur et les satellites d’après l’Équation 3 sont donc :

Les satellites GPS sont entre 10 000 et 20 000km d'altitude par rapport à la surface de la terre. Il faut rajouter le rayon de la terre (6371 km) pour avoir leur distance par rapport au centre de la terre.

donc :

Avec nos données, les altitudes pour cet exemple sont :

En mettant l’Équation 3 au carré, on obtient

Comme l’on nous donne les temps de propagation dt_i = (t-t_i), cela nous donne :

En développant :

Donc, avec les 4 satellites :

Avec nos données, cela donne :

Soit :

En soustrayant (Eq5) et (Eq4), (Eq6) et (Eq4), (Eq7) et (Eq4), on obtient un système d’équation sans x² , y² :

donc :

donc :

donc :

On obtient un système de trois équations à trois inconnues.

On isole x dans la première équation :

donc :

donc :

donc :

donc :

On isole y dans l'équation (EqD) :

donc :

soit :

soit :

Ce qui donne :

et pour finir :

On peut en conclure que le récepteur se trouve aux coordonnées x=4210 y=-99 et z=4790. Ces coordonnées sont approximatives car les coordonnées satellites pour cet exemple sont arrondis au km près.

Vérifions à quelle distance du centre de la terre se trouve le récepteur :

Le rayon de la terre étant de 6371 km, le récepteur GPS se trouve bien sur terre !

Ces coordonnées peuvent être ensuite exprimées par le GPS en longitude latitude et altitude.

3) Un manque de précision :

a.      Ralentissement de 7,2μs

On sait que le GPS traite du sujet de la relativité énoncé par Einstein et en particulier un phénomène : la dilatation du temps, que nous avons évoqué avant. Ici dans la relativité restreinte il consiste à affirmer que le temps s’écoule plus lentement lorsque qu’un objet se déplace à une grande vitesse, alors que dans la relativité générale cela consiste à un écoulement plus rapide du temps lorsque l’objet se trouve à une grande distance d'un astre.

La dilatation du temps dans l’espace est du à une vitesse élevée des satellites et des horloges atomiques embarquées à l’intérieur. Celle-ci réduit le temps de propagation de la fréquence électromagnétique. On peut prendre la loi de composition des vitesses :

T'=T

=1/(√(1-U²/c²))

Données :

T=1 jour = 8,64 × 10⁴ s

Vitesse du satellite : U=14 000 km/h ≈ 3889 m/s

Calculs : 

T'=1/(√(1-3889²/(3,0×10⁸)²) × 8,64 × 10⁴

T'=1,000000000084 × 8,64 × 10⁴

T'=86400,000007258 s = 8640000000725,8 µs

T' - T = 86400,000007258 - 8,64 × 10⁴ = 7,26 × 10^-6 s = 7,26 µs

On obtient un ralentissement de 7,2µs/jour.

Autrement dit, le temps s’écoule plus lentement de 7,2µs/jour au niveau des satellites par rapport au sol, à cause de la vitesse des satellites.

b.      Accélération de 45,6μs

Calculons maintenant l'effet de la relativité générale. Comme on l'a vu précédemement : plus on est proche d'un corps massif, moins le temps s'écoule. C'est la dilatation du temps d'origine gravitationnelle.

Pour rappel, le décalage relatif entre une horloge à la surface d'une sphère de masse M et de rayon R et une horloge d'altitude h est donné par : 

?f/f = (GM)/c² × (1/R-1/(R+h))

Données :

G = 6,674 × 10⁻¹¹ m³ · kg⁻¹ · s⁻²

M = 5,972 × 10²⁴ kg

c = 3,0 × 10⁸ m/s

R = 6371 km (le rayon de la terre) = 6,371 × 10⁶ m

h = 20200 km (au dessus de la surface de la terre) = 20,200 × 10⁶ m

Calcul : 

?f/f = (GM)/c² × (1/R-1/(R+h)) = 6,674 × 10⁻¹¹ × 5,972 × 10²⁴ / (3,0 × 10⁸)² × (1/(6,371 × 10⁶)-1/(6,371 × 10⁶+20,200 × 10⁶))

?f/f = 5,28 × 10⁻¹⁰

Le temps au niveau du satellite "avance plus vite" de 5,28 × 10⁻¹⁰ secondes par second par rapport au sol.

Pour 1 journée, soit 24 × 3600s, ce décallage est de 4,56 × 10⁻⁵ s

Autrement dit, le temps s’écoule plus vite d'environ 45,6 µs/jour au niveau des satellites par rapport au sol, à cause de l'effet gravitationnel

c.      Un manque de précision de 11,5 km/jour

Par un calcul simple (45,65 – 7,26 = 38,4), le temps s’écoule donc plus vite d'environ 38,4 µs/jour au niveau des satellites par rapport au sol.

D=c*?t = 3,0 × 10⁸ × 38,4, × 10⁻⁵ = 11520 m

Sans rattrappage d'erreur, le GPS dérive donc de 11,5 km par jour à cause des deux effets relativistes.